Homepage Fundamental
Research Intro Families Applied Research
Mass Production Connectors Covering Air lifted Light Structures Projects Gallery Contact News Publishing Guestbook FAQ Contact
printed from www.equilatere.net
The family CUB
1/ Generalities
1.1/ The origin : A module composed of modules (again).
Here is the second family of closed forms. By this, I mean forms closed within themselves. This idea came to me when I first noticed that family C6 forms were sufficiently flexible to adopt certain proportions allowing them to surround a cub.
I would first like to take the opportunity here, across a two thousand year span, to address my most grateful and respectful thanks to Plato, and consequently to Socrate who was his master and Aristote who was his disciple.
This family is thus the second of my families (there are others) to establish a connection with platonic volumes. To illustrate the explanation, I used the form 45P45P2.C6, but I could have used form 45P45P3.C6 or P4 or P5, etc. (See C6 family)
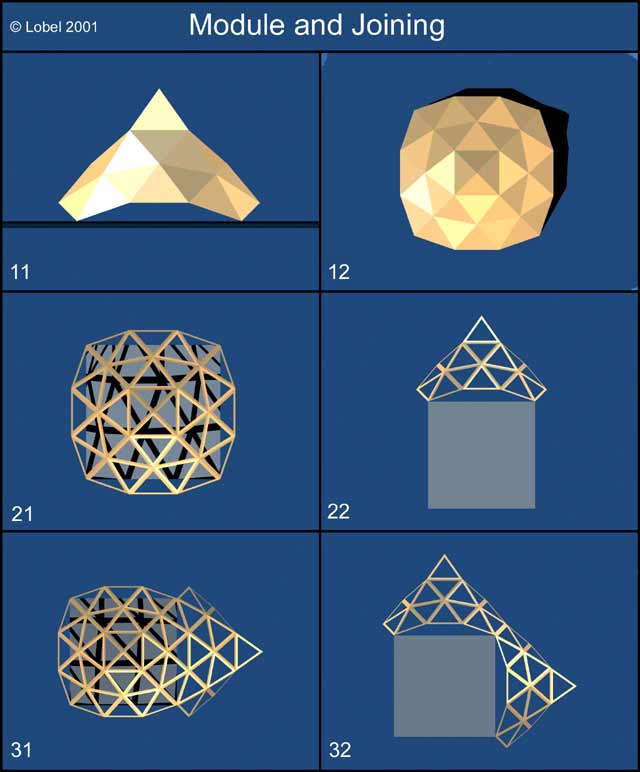
This form is interesting in this particular case because its four suspension points can rest on each vertex of the square that make up the cub. I calculated the slope of the angle at 45° which is (as any geodesic-man knows..) the half angle that makes up the faces of the cub...! (Figures: Module and Joining - the classic sights)
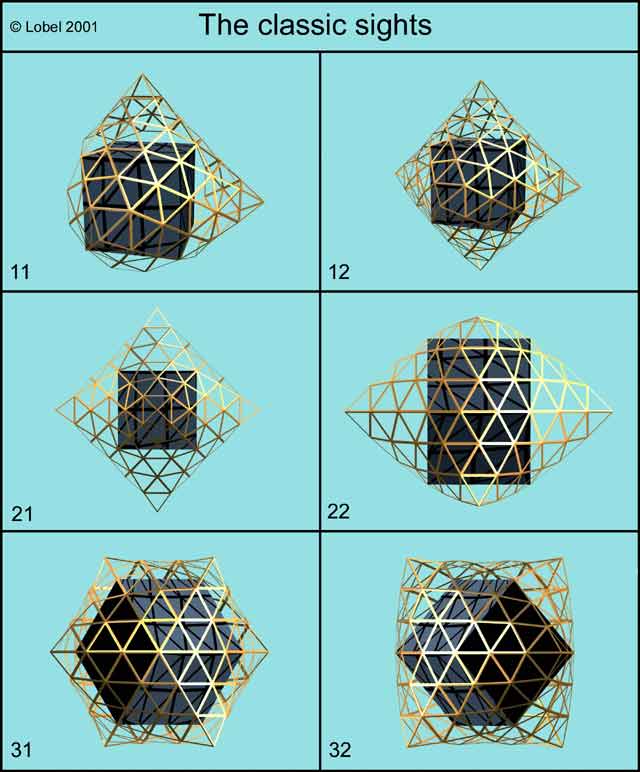
The shapes are then placed on each faces of the cub. As their openings line up joining perfectly, a closed volume with three orthogonally symmetric planes is formed. I call this shape "the mother shape". Each tip of this form is inscribed in a sphere.
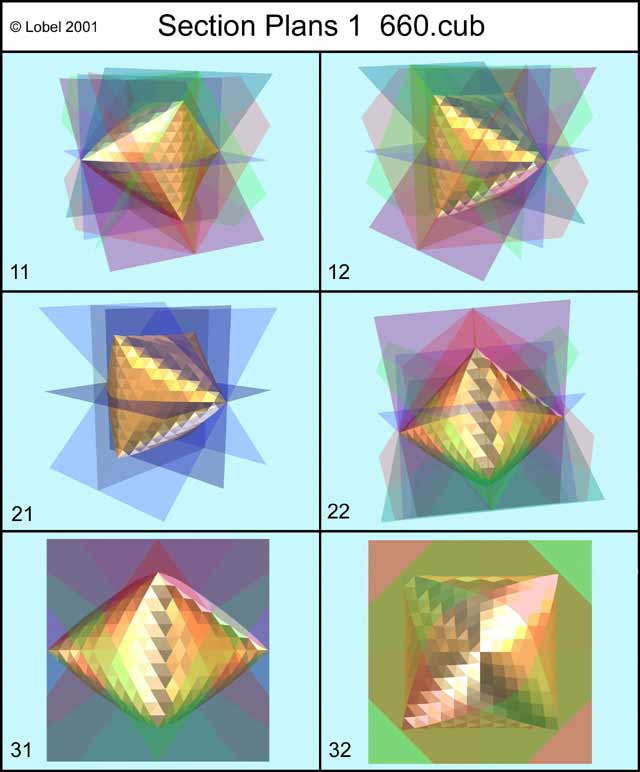
This mother shape has twelve symmetrical planes in which only two are interesting as the others are just repetitions. (Figure Section plane 1)
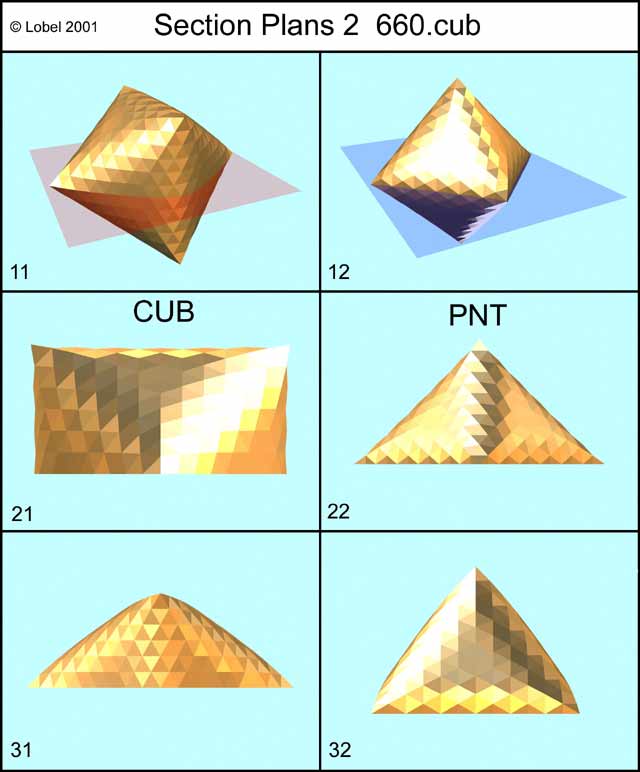
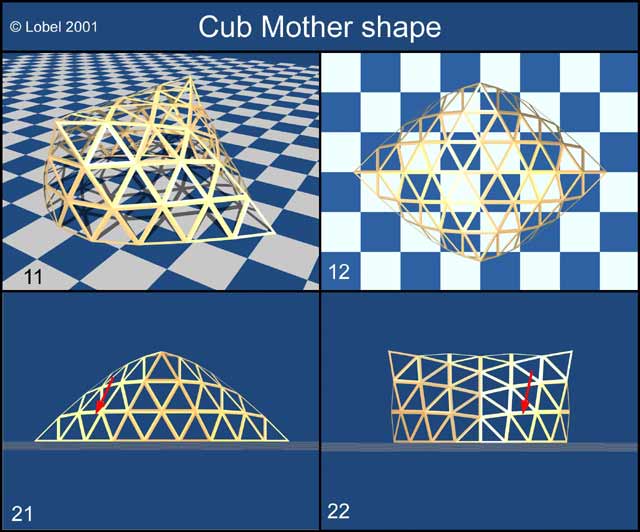
By cutting it by both of its principal perpendicular symmetrical planes, I get two different families, CUB and PNT. (Figure Section Plane 2 and Cub Mother shape).
I will now speak more particularly about the CUB family. I will later write a specific chapter about the PNT family and its developments.
1.2/ Diversification
After having cut the mother form by its symmetrical plane, the shape lies completely on a plane.
If we consider each vertex as being articulated, the half form is not rigid in itself, but thanks to the miracle of the god of structures, we easily understand when the base line is rigid, either because it is fixed on the plane (on the ground) or by any other means of rigidifying the line, the entire form becomes completely inflexible. Of course, by this I mean geometrically rigid (which is already considerable).
The materials, being pliable, do not behave (alas, or so much the better!) like perfect straight lines in geometry.
When carefully examining mother shape n°21 et n°22, one notices (see arrow) that the broken line directly under the one on the ground is not quite horizontal. As in the preceding CSM family case, I strung out this line towards the horizontal.
1.3/ Architectural remarks
Among all the families studied, notice that forms stemming from the CUB family are those in which the right angle has the greatest impression.
Volumes are found in which ground surfaces are inscribed in a rectangle (or nearly, see catalog 650/x, 645/x and z, 635/x, 563/x, 560/x etc.). Surprisingly, by wanting to get away from the right angle it catches up on me, which is rather a good thing as it has lost its depressing monotony. Volumes can thus be used within the framework of numerous traditional activities such as warehouses, studios, garages, tennis courts, etc...
1.1/ The origin : A module composed of modules (again).
Here is the second family of closed forms. By this, I mean forms closed within themselves. This idea came to me when I first noticed that family C6 forms were sufficiently flexible to adopt certain proportions allowing them to surround a cub.
I would first like to take the opportunity here, across a two thousand year span, to address my most grateful and respectful thanks to Plato, and consequently to Socrate who was his master and Aristote who was his disciple.
This family is thus the second of my families (there are others) to establish a connection with platonic volumes. To illustrate the explanation, I used the form 45P45P2.C6, but I could have used form 45P45P3.C6 or P4 or P5, etc. (See C6 family)
This form is interesting in this particular case because its four suspension points can rest on each vertex of the square that make up the cub. I calculated the slope of the angle at 45° which is (as any geodesic-man knows..) the half angle that makes up the faces of the cub...! (Figures: Module and Joining - the classic sights)

The shapes are then placed on each faces of the cub. As their openings line up joining perfectly, a closed volume with three orthogonally symmetric planes is formed. I call this shape "the mother shape". Each tip of this form is inscribed in a sphere.

This mother shape has twelve symmetrical planes in which only two are interesting as the others are just repetitions. (Figure Section plane 1)

By cutting it by both of its principal perpendicular symmetrical planes, I get two different families, CUB and PNT. (Figure Section Plane 2 and Cub Mother shape).
I will now speak more particularly about the CUB family. I will later write a specific chapter about the PNT family and its developments.
1.2/ Diversification
After having cut the mother form by its symmetrical plane, the shape lies completely on a plane.
If we consider each vertex as being articulated, the half form is not rigid in itself, but thanks to the miracle of the god of structures, we easily understand when the base line is rigid, either because it is fixed on the plane (on the ground) or by any other means of rigidifying the line, the entire form becomes completely inflexible. Of course, by this I mean geometrically rigid (which is already considerable).
The materials, being pliable, do not behave (alas, or so much the better!) like perfect straight lines in geometry.

When carefully examining mother shape n°21 et n°22, one notices (see arrow) that the broken line directly under the one on the ground is not quite horizontal. As in the preceding CSM family case, I strung out this line towards the horizontal.
1.3/ Architectural remarks
Among all the families studied, notice that forms stemming from the CUB family are those in which the right angle has the greatest impression.
Volumes are found in which ground surfaces are inscribed in a rectangle (or nearly, see catalog 650/x, 645/x and z, 635/x, 563/x, 560/x etc.). Surprisingly, by wanting to get away from the right angle it catches up on me, which is rather a good thing as it has lost its depressing monotony. Volumes can thus be used within the framework of numerous traditional activities such as warehouses, studios, garages, tennis courts, etc...
