Homepage Fundamental
Research Intro Families Applied Research
Mass Production Connectors Covering Air lifted Light Structures Projects Gallery Contact News Publishing Guestbook FAQ Contact
printed from www.equilatere.net
Description
Je commence maintenant la description de chacune des familles que j'ai identifié. Je respecterai l'ordre chronologique des découvertes et j'indiquerai les caractéristiques distinctives de chacune de ces familles ainsi que les lois qui les gouvernent.
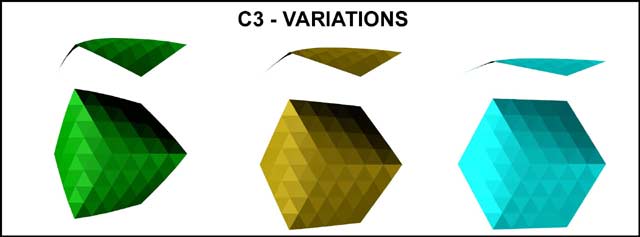
La première famille de formes que j'ai identifié est la C3.
C'est elle qui m'a convaincu que l'assemblage de triangles équilatéraux était capable de générer d'autres volumes que les volumes platoniciens connus, c'est à dire: le tétraèdre, l'octaèdre, et l'icosaèdre.
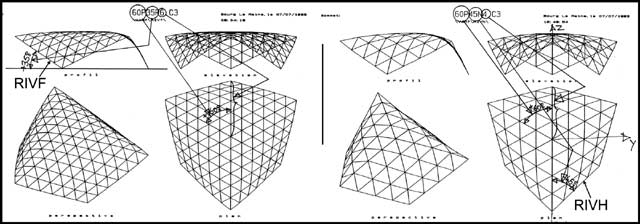
Il est possible d'imposer une direction à chacune des barres de rive, en particulier une direction telle que toutes les barres de rive, bien que n'étant pas dans le prolongement l'une de l'autre, apparaissent en projection sur le plan horizontal comme une seule droite projetée.
J'ai appelé cette sous famille RIVH
La même réflexion m'a conduit a imaginer que, puisque c'était possible en projection sur le plan horizontal ça devait l'être aussi en projection sur le plan frontal.
J'ai appelé cette sous famille RIVF
Le dessin qui suit l'explique et définit en même temps l'appellation des formes.
Je commence maintenant la description de chacune des familles que j'ai identifié. Je respecterai l'ordre chronologique des découvertes et j'indiquerai les caractéristiques distinctives de chacune de ces familles ainsi que les lois qui les gouvernent.
La première famille de formes que j'ai identifié est la C3.
C'est elle qui m'a convaincu que l'assemblage de triangles équilatéraux était capable de générer d'autres volumes que les volumes platoniciens connus, c'est à dire: le tétraèdre, l'octaèdre, et l'icosaèdre.
Il est possible d'imposer une direction à chacune des barres de rive, en particulier une direction telle que toutes les barres de rive, bien que n'étant pas dans le prolongement l'une de l'autre, apparaissent en projection sur le plan horizontal comme une seule droite projetée.
J'ai appelé cette sous famille RIVH
La même réflexion m'a conduit a imaginer que, puisque c'était possible en projection sur le plan horizontal ça devait l'être aussi en projection sur le plan frontal.
J'ai appelé cette sous famille RIVF
Le dessin qui suit l'explique et définit en même temps l'appellation des formes.
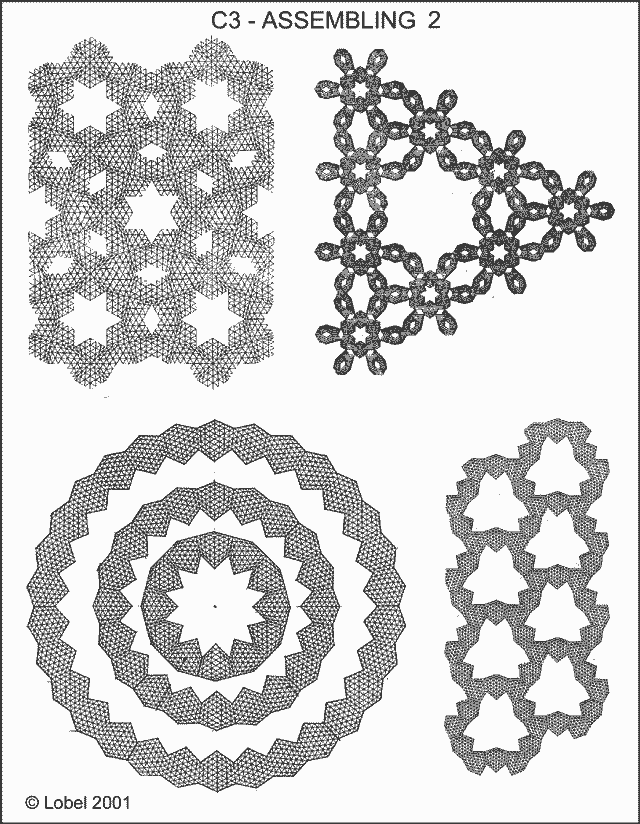
Dans ces 2 cas on peut faire varier l'angle des droites projetées et obtenir ainsi des formes plates ou creuses possédant des propriétés d'association entre elles, comme le montrent les images suivantes.