Homepage Fundamental
Research Intro Families Applied Research
Mass Production Connectors Covering Air lifted Light Structures Projects Gallery Contact News Publishing Guestbook FAQ Contact
printed from www.equilatere.net
2/ Appellation des formes
En ce qui concerne la famille CSM j'ai défini 4 paramètres principaux F, F1, F2, F3 (shapes titling n°11) qui expriment des fréquence (J'ai repris ce terme de fréquence par analogie avec les termes utilisés dans les structures géodésiques classiques.). D'une manière générale plus les fréquences sont élevées et plus il y a de triangles dans la forme. Comme la forme est divisée en plusieurs zones dépendant de ces fréquences, lorsque l'on fait varier ces mêmes fréquences, on peut ainsi l'étirer dans une zone et la compresser dans une autre.
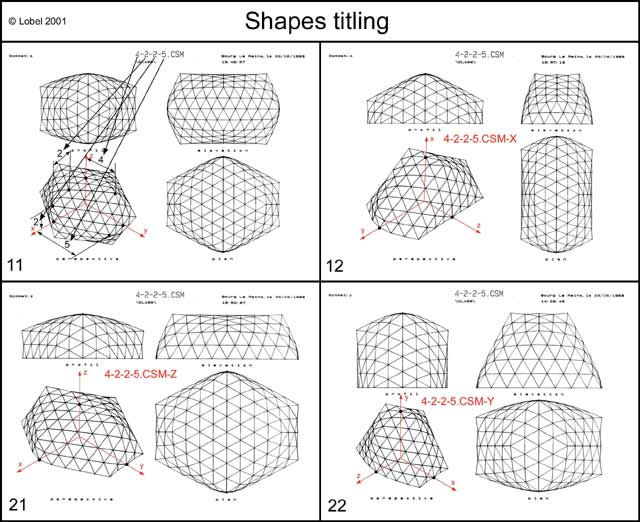
Comme chacune de ces formes repose sur un plan, en la symétrisant par rapport à ce plan, on obtient une forme close qui possède toujours 3 plans de symétrie orthogonaux. Ainsi ce nouveau volume clos peut à son tour être coupé selon ses 3 plans de symétrie orthogonaux. Un volume clos donnant donc naissance à 3 volumes reposant sur des plans parfaits.
Un de mes étudiants a comparé ça à des patates de formes variées que l'on couperait selon 3 plans orthogonaux.
Il a donc fallu distinguer par des appellations différentes ces 3 formes venant du même volume clos (la même patate!). J'ai donc adopté le nom de la forme générale suivi de X, Y ou Z selon l'axe qui la traversait en partie haute. Ainsi, la forme générale appelée 4225 devient dans ses 3 déclinaisons 4225-X, 4225-Y, 4225-Z. (ouf!).
En ce qui concerne la famille CSM j'ai défini 4 paramètres principaux F, F1, F2, F3 (shapes titling n°11) qui expriment des fréquence (J'ai repris ce terme de fréquence par analogie avec les termes utilisés dans les structures géodésiques classiques.). D'une manière générale plus les fréquences sont élevées et plus il y a de triangles dans la forme. Comme la forme est divisée en plusieurs zones dépendant de ces fréquences, lorsque l'on fait varier ces mêmes fréquences, on peut ainsi l'étirer dans une zone et la compresser dans une autre.

Comme chacune de ces formes repose sur un plan, en la symétrisant par rapport à ce plan, on obtient une forme close qui possède toujours 3 plans de symétrie orthogonaux. Ainsi ce nouveau volume clos peut à son tour être coupé selon ses 3 plans de symétrie orthogonaux. Un volume clos donnant donc naissance à 3 volumes reposant sur des plans parfaits.
Un de mes étudiants a comparé ça à des patates de formes variées que l'on couperait selon 3 plans orthogonaux.
Il a donc fallu distinguer par des appellations différentes ces 3 formes venant du même volume clos (la même patate!). J'ai donc adopté le nom de la forme générale suivi de X, Y ou Z selon l'axe qui la traversait en partie haute. Ainsi, la forme générale appelée 4225 devient dans ses 3 déclinaisons 4225-X, 4225-Y, 4225-Z. (ouf!).