Homepage Fundamental
Research Intro Families Applied Research
Mass Production Connectors Covering Air lifted Light Structures Projects Gallery Contact News Publishing Guestbook FAQ Contact
printed from www.equilatere.net
La famille CUB
1/ Généralités
1.1/ L'origine: Un module encore composé de modules.
Voici maintenant la seconde famille de formes closes à établir une connexion avec les volumes platoniciens.
On me permettra ici, à travers 2 millénaires, d'adresser un salut amical, reconnaissant et respectueux à Platon et par conséquent à Socrate qui fut son maître et Aristote qui fut son disciple. Pour les besoins de l'explication j'ai utilisé la forme 45P45P2.C6, mais j'aurai pu utiliser aussi bien 45P45P3 ou P4 ou P5 ...etc.
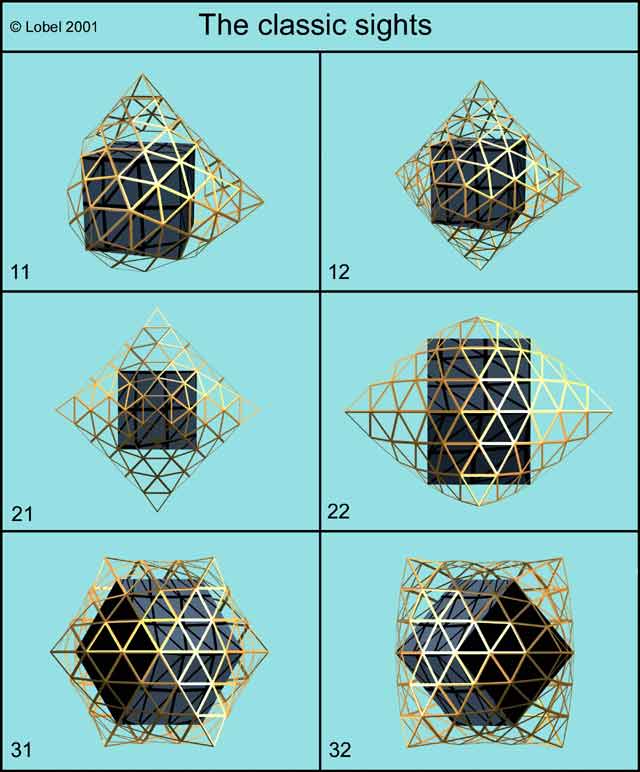
Cette forme est intéressante dans ce cas particulier car elle possède 4 points d'appui qui peuvent donc reposer sur les sommets de chacun des carrés qui composent le cube. J'ai donc réglé par le calcul, l'inclinaison du plan d'ouverture de cette forme à l'angle de 45° qui est (comme chaque géodésique-man le sait :-) le demi angle que font les faces d'un cube. (Figure: Module and Joining - the classic sights)
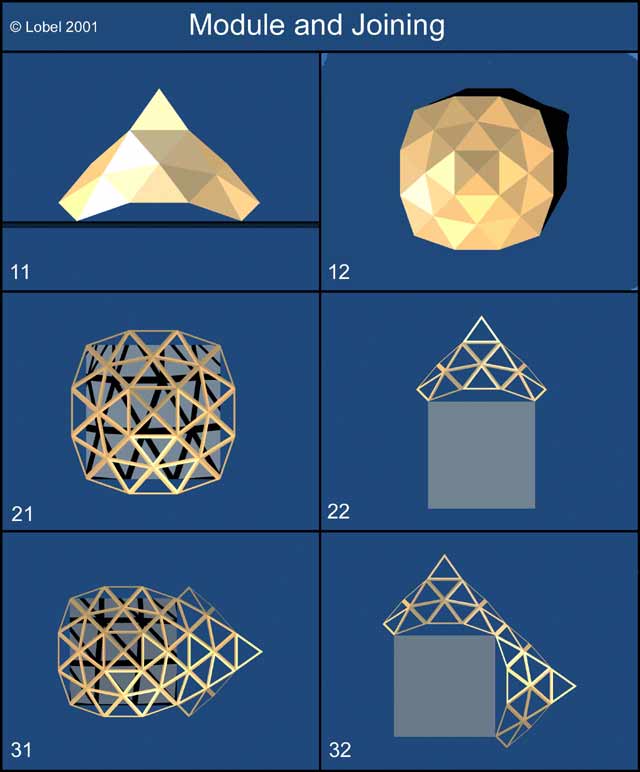
Il n'y avait plus qu'à les poser sur chacune des faces du cube. Comme leurs ouvertures se joignent exactement on obtient immédiatement un volume clos. J'appelle encore ce volume forme mère. Chacune des pointes de cette forme est donc inscrite dans une sphère.
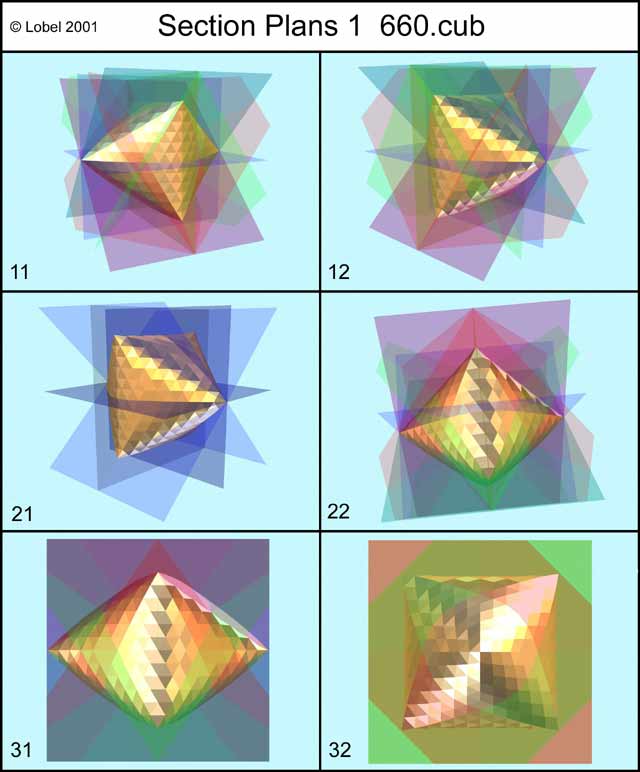
Cette forme mère possède 12 plans de symétrie dont 2 seulement sont interressants car les autres ne sont que des répétitions. (Figure Section Plans 1)
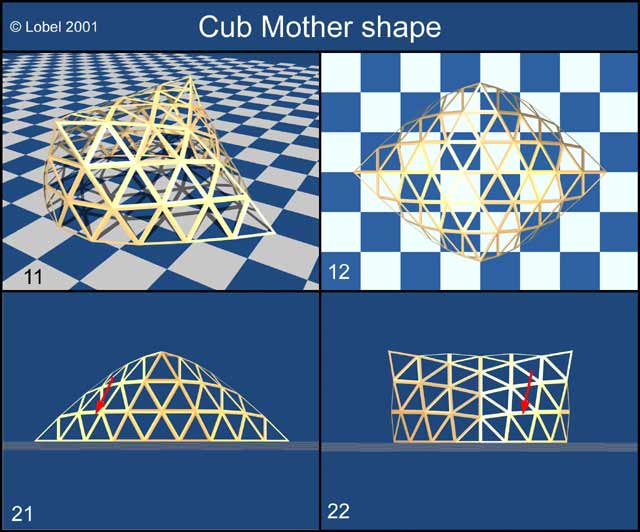
En la coupant par chacun de ses 2 plans de symétrie perpendiculaires principaux, j'obtiens 2 familles différentes, CUB et PNT. (Figure Section Plans 2 and Cub Mother shape)
Je parlerai ici plus spécialement de la famille CUB. Plus tard je ferai un chapitre spécial pour la PNT et ses développements.
1.2/ La diversification
Après avoir coupé la forme mère par son plan de symétrie, la forme repose donc complètement sur un plan.
Si l'on considère chaque sommet comme étant articulé cette demie forme ne possède pas de rigidité par elle même, mais, par le miracle du dieu des structures, (air connu) on comprendra facilement que lorsque la ligne de la base est rigide, soit parce qu'elle est fixée sur le plan (sur le sol), soit parce que, par un moyen quelconque, on a rigidifié cette ligne , alors l'ensemble de la forme devient complètement rigide. Je veux dire, bien sur, géométriquement rigide (mais c'est déjà quelque chose). Les matériaux étant élastiques ne se comportent pas (hélas ou tant mieux!) comme les droites parfaites de la géométrie.
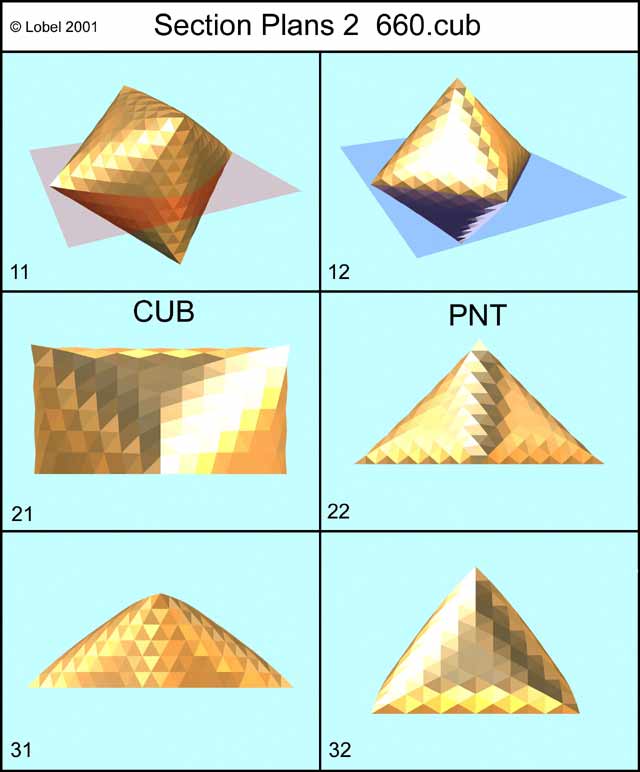
Si l'on observe attentivement la figure: the mother shape n°21 et 22, on constatera (flèche) que la ligne brisée, immédiatement au dessus de celle reposant sur le sol, n'est pas horizontale mais elle en est assez proche. Comme dans le cas de la famille CSM précédente, j'ai donc fait tendre cette ligne vers l'horizontale.
1.3/ Remarques architecturales
Parmi toutes les familles étudiées, il faut remarquer que les formes issues de la famille CUB sont celles qui portent le plus l'empreinte de l'angle droit.
On y trouve des volumes dont la surface au sol s'inscrit dans un rectangle (ou presque, voir catalogue 650/x, 645/x et z, 635/x, 563/x, 560/x etc). Etonnamment, en voulant échapper à l'angle droit, celui ci me rattrape, mais c'est plutôt un bien car il a perdu ici sa monotonie déprimante et les volumes peuvent être utilisés dans le cadre de nombreuse activités traditionnelles comme entrepôts, ateliers, garages, Tennis, etc ...
1.1/ L'origine: Un module encore composé de modules.
Voici maintenant la seconde famille de formes closes à établir une connexion avec les volumes platoniciens.
On me permettra ici, à travers 2 millénaires, d'adresser un salut amical, reconnaissant et respectueux à Platon et par conséquent à Socrate qui fut son maître et Aristote qui fut son disciple. Pour les besoins de l'explication j'ai utilisé la forme 45P45P2.C6, mais j'aurai pu utiliser aussi bien 45P45P3 ou P4 ou P5 ...etc.
Cette forme est intéressante dans ce cas particulier car elle possède 4 points d'appui qui peuvent donc reposer sur les sommets de chacun des carrés qui composent le cube. J'ai donc réglé par le calcul, l'inclinaison du plan d'ouverture de cette forme à l'angle de 45° qui est (comme chaque géodésique-man le sait :-) le demi angle que font les faces d'un cube. (Figure: Module and Joining - the classic sights)

Il n'y avait plus qu'à les poser sur chacune des faces du cube. Comme leurs ouvertures se joignent exactement on obtient immédiatement un volume clos. J'appelle encore ce volume forme mère. Chacune des pointes de cette forme est donc inscrite dans une sphère.

Cette forme mère possède 12 plans de symétrie dont 2 seulement sont interressants car les autres ne sont que des répétitions. (Figure Section Plans 1)

En la coupant par chacun de ses 2 plans de symétrie perpendiculaires principaux, j'obtiens 2 familles différentes, CUB et PNT. (Figure Section Plans 2 and Cub Mother shape)
Je parlerai ici plus spécialement de la famille CUB. Plus tard je ferai un chapitre spécial pour la PNT et ses développements.
1.2/ La diversification
Après avoir coupé la forme mère par son plan de symétrie, la forme repose donc complètement sur un plan.
Si l'on considère chaque sommet comme étant articulé cette demie forme ne possède pas de rigidité par elle même, mais, par le miracle du dieu des structures, (air connu) on comprendra facilement que lorsque la ligne de la base est rigide, soit parce qu'elle est fixée sur le plan (sur le sol), soit parce que, par un moyen quelconque, on a rigidifié cette ligne , alors l'ensemble de la forme devient complètement rigide. Je veux dire, bien sur, géométriquement rigide (mais c'est déjà quelque chose). Les matériaux étant élastiques ne se comportent pas (hélas ou tant mieux!) comme les droites parfaites de la géométrie.

Si l'on observe attentivement la figure: the mother shape n°21 et 22, on constatera (flèche) que la ligne brisée, immédiatement au dessus de celle reposant sur le sol, n'est pas horizontale mais elle en est assez proche. Comme dans le cas de la famille CSM précédente, j'ai donc fait tendre cette ligne vers l'horizontale.
1.3/ Remarques architecturales
Parmi toutes les familles étudiées, il faut remarquer que les formes issues de la famille CUB sont celles qui portent le plus l'empreinte de l'angle droit.
On y trouve des volumes dont la surface au sol s'inscrit dans un rectangle (ou presque, voir catalogue 650/x, 645/x et z, 635/x, 563/x, 560/x etc). Etonnamment, en voulant échapper à l'angle droit, celui ci me rattrape, mais c'est plutôt un bien car il a perdu ici sa monotonie déprimante et les volumes peuvent être utilisés dans le cadre de nombreuse activités traditionnelles comme entrepôts, ateliers, garages, Tennis, etc ...
