Homepage Fundamental
Research Intro Families Applied Research
Mass Production Connectors Covering Air lifted Light Structures Projects Gallery Contact News Publishing Guestbook FAQ Contact
printed from www.equilatere.net
2/ Shapes designation
I defined four principal parameters; F, F1, F2, F3 (shapes titling n°11) for the CSM family which expressed the frequency (I took this frequency term by analogy to terms used in classic geodesic structures). In general, the higher the frequency, more numerous are the triangles in the form. As the form is divided into many zones depending on the frequencies, when these same frequencies are varied, zones can consequently be stretched or compressed.
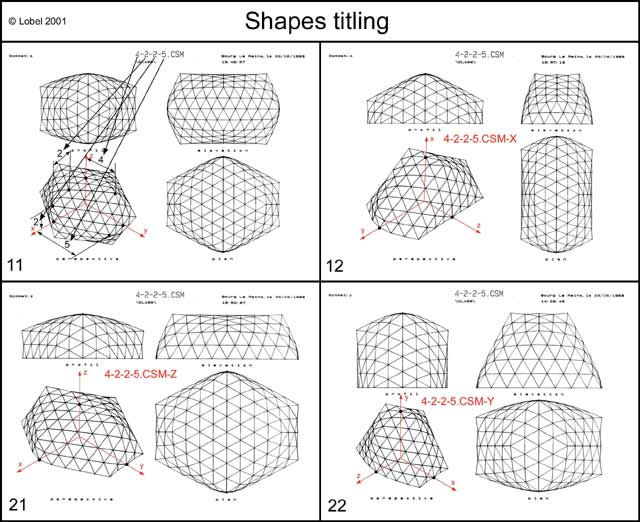
As each of these forms lie on a plane, by making it symmetrical in relation to this plane, a closed form is obtained possessing three orthogonal symmetrical planes. In this way, this new closed volume can also be cut according to its three orthogonal symmetrical planes. So one closed volume generates three volumes lying on perfect planes.
One of my students compared this to variously shaped potatoes that are cut on three orthogonal planes (try this and then, in order to not waste them, cut them in small cubes which you then fry in a pan with bacon, it's delicious; we call this sauteed potatoes).
These three forms coming from the same closed volume (the potato!) had to be distinguished by different names. I thus adopted the name of the general form followed by X, Y, or Z according to the axis which goes through it at the higher part. And so the three declinations of general form 4225 become 4225-X, 4225-Y, 4225-Z. (phew!).
It is now easier to understand the mother shape declination plate.
I defined four principal parameters; F, F1, F2, F3 (shapes titling n°11) for the CSM family which expressed the frequency (I took this frequency term by analogy to terms used in classic geodesic structures). In general, the higher the frequency, more numerous are the triangles in the form. As the form is divided into many zones depending on the frequencies, when these same frequencies are varied, zones can consequently be stretched or compressed.

As each of these forms lie on a plane, by making it symmetrical in relation to this plane, a closed form is obtained possessing three orthogonal symmetrical planes. In this way, this new closed volume can also be cut according to its three orthogonal symmetrical planes. So one closed volume generates three volumes lying on perfect planes.
One of my students compared this to variously shaped potatoes that are cut on three orthogonal planes (try this and then, in order to not waste them, cut them in small cubes which you then fry in a pan with bacon, it's delicious; we call this sauteed potatoes).
These three forms coming from the same closed volume (the potato!) had to be distinguished by different names. I thus adopted the name of the general form followed by X, Y, or Z according to the axis which goes through it at the higher part. And so the three declinations of general form 4225 become 4225-X, 4225-Y, 4225-Z. (phew!).
It is now easier to understand the mother shape declination plate.